


Sometimes the application of Lagrange equation to a variable system may result in a system of nonlinear partial differential equations. Navier-Stokes equation and Euler’s equation in fluid dynamics, Einstein’s field equations of general relativity are well known nonlinear partial differential equations. Therefore, each equation has to be treated independently. In case of partial differential equations, most of the equations have no general solution. Nonlinear differential equations are difficult to solve, therefore, close study is required to obtain a correct solution. What is a Nonlinear Differential Equation?Įquations that contain nonlinear terms are known as non-linear differential equations.Īll above are nonlinear differential equations. Newton’s second law produces a second order linear differential equation with constant coefficients. Classic example for this case is Newton’s second law of motion and its various applications. The easiest case arises when the coefficients are constant. Solution method for the differential equation is dependent on the type and the coefficients of the differential equation. If f is a function of two or more independent variables (f: X,T→Y) and f(x,t)=y, then the equation is a linear partial differential equation. If the function is g=0 then the equation is a linear homogeneous differential equation. The linearity of the equation is only one parameter of the classification, and it can further be categorized into homogenous or non-homogenous and ordinary or partial differential equations. That is, if y 1 and y 2 are solutions of the differential equation, then C 1 y 1+ C 2 y 2 is also a solution. As a result of the linear nature of the solution set, a linear combination of the solutions is also a solution to the differential equation. In a linear differential equation, the differential operator is a linear operator and the solutions form a vector space. The equation is a differential equation of order n, which is the index of the highest order derivative. It also cannot contain non linear terms such as Sin y, e y^-2, or ln y. It takes the form,

It imposes the condition that y cannot have higher index terms such as y 2, y 3 ,… and multiples of derivatives such as Suppose that f: X→Y and f(x)=y, a differential equation without nonlinear terms of the unknown function y and its derivatives is known as a linear differential equation. It is important to identify the difference between linear and nonlinear differential equations. Linear and nonlinear is one such categorization. Therefore, for easier identification differential equations are categorized by their mathematical behaviour.
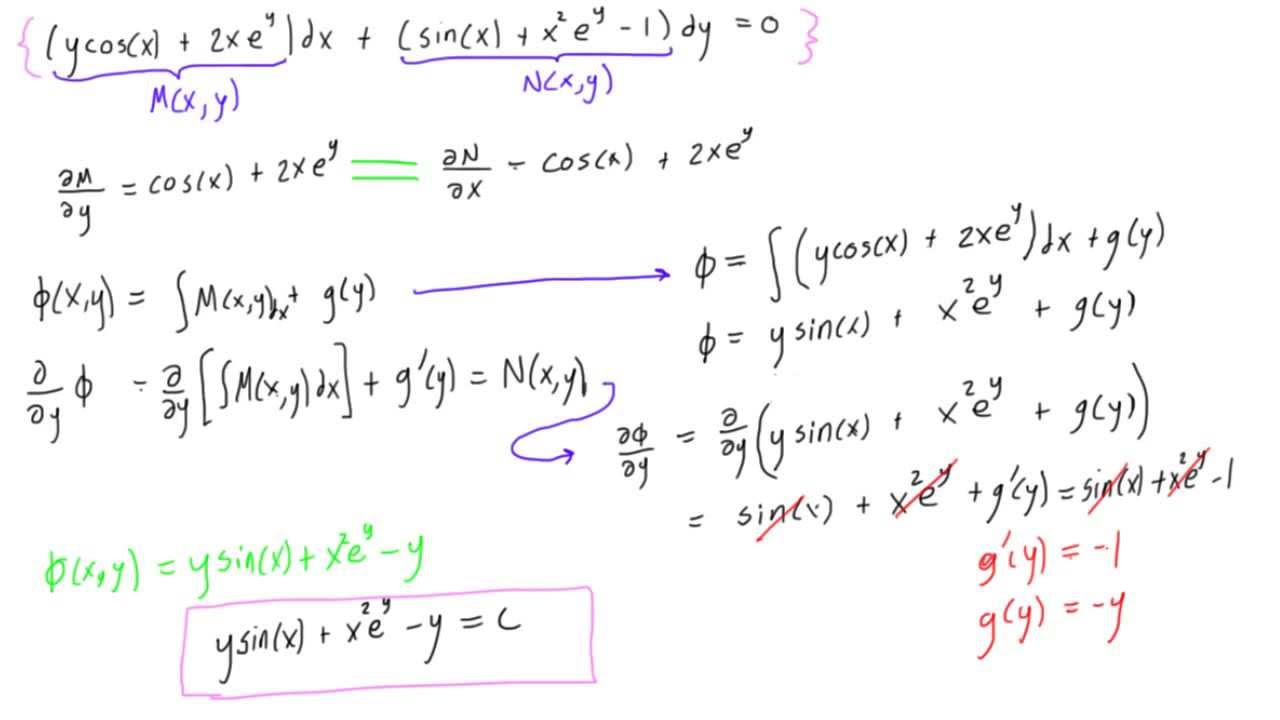
However, there are ones that we can solve, but may look alike and confusing. Resulting equations from a specific application of calculus may be very complex and sometimes not solvable. In fact, until calculus became an established theory, proper mathematical tools were unavailable to analyze the interesting problems in the nature. Differential equations are at the heart of every model we develop to explain any scenario or event in the world whether it is in physics, engineering, chemistry, statistics, financial analysis, or biology (the list is endless). Differential equations are of great importance in mathematics because of their range of applications. Since the development of calculus in the 18th century by the mathematicians like Newton and Leibnitz, differential equation has played an important role in the story of mathematics. The scope of this article is to explain what is linear differential equation, what is nonlinear differential equation, and what is the difference between linear and nonlinear differential equations. A differential equation can be either linear or non-linear. In $(3)$ we have the saddle case again, unstable.Linear vs Nonlinear Differential EquationsĪn equation containing at least one differential coefficient or derivative of an unknown variable is known as a differential equation. In $(2)$real parts are both negative so I have an attractor point that is stable. In $(1)$real parts are both positive so I have a repellor point that is unstable. The number of equilibria has jumped from none to four! To see this, note that now $x' = y' = 0$ implies, from (1), (2), that Well, I ain't no $Moshe$ but I can cut some down some of the work, thus: Where is Moshe now that we need him to lead us out from under Pharoah's toil? This answer posted in response to the modified system, given in (1) and (2) below:


 0 kommentar(er)
0 kommentar(er)
